等式の変形 解き方 322213-等式の変形 解き方 分数

1

等式の変形 等式 xy=5 を x=5 y に変形したり， S= ah2nn を h= 2Sann に変形することは， 次に習う方程式の解き方において基本となる技術です． 問題 次の等式を 内に示された文字について解きなさい． x−y=3 の x を右辺に移項する． __________ −y=−x3 両辺に −1 を掛ける． __________ y=x−3 →閉じる← （2） v=sh h について h= nn v=sh の左辺と右辺を入れ替える． __________等式の変形とは 0：15 等式の変形とは、 等式の性質 を使って変形して、指定された文字について 解く ことをいいます。 等式変形は、いろいろな単元の問題や解説に出てくるので、しっかり確認していきましょう。 例えば、 2 x y = 5 ( 2 元 1 次方程式) を

等式の変形 解き方 分数

等式の変形 解き方 分数- 対数方程式・不等式の解き方 問題はこちら。 （1）の解答 まずおさえて欲しいのはとにかく数字を対数にすることです。今回の問題は \(\log_{3}{(x2)}=2\) ですが、これは右辺を底が \(3\) の対数にできれば問題が解けそうです。解き方 2 x 7 = 13 まずは x = の形にしたいので、 x だけ左辺に残すように、左辺の数字を0にします。 この問題の場合は 7が邪魔なので、 7に 7をして 0にします。 この時、上の等式の性質の考え方を使い左辺と同じ計算を右辺にもします。 （下の式なら 7の部分） 2 x 7 − 7 = 13 − 7 2 2 2 x ÷ 2 = 6 ÷ 2 2 x となっていますので、 x の係数 2を 1にします。 1にするためには、係

等式の性質とは 方程式を解くための考え方を身につけよう 方程式の解き方まとめサイト

 等式変形について苦手意識をもっている人、やり方がわからない人は解く際の参考にして下さい。 スポンサーリンク 中1数学 等式の性質 ―4つの性質をマスターしましょう。 方程式の変形は、「1行上の等式が成り立っているとすると、この等式も成り立っている」という考えで変形しています。 「 $3x1$ と $100$ が等しいなら、それぞれ $1$ を取り除いても等しい」ため、1行目から2行目へと変形しているわけですね。等式の変形の解き方・\ (3\)ステップ \ (1\)、解く文字の式を左辺に移す \ (2\)、解く文字に足した式を移項する \ (3\)、解く文字に掛けた式を割る 等式の変形のポイントと解き方を見ていきましょう。 等式の変形のポイント 等式の変形のポイントは次の

 こういう時は右辺と左辺の 両方の式を式変形して一致させる ことで証明します。 から となり左辺の式変形からします。 となります。 文字が3種類以上ある時の展開はこうする の式変形ですが多項定理を使って展開するのは面倒ですよね。 (意味が分からなかったら気にしなくていいです) これは知識として知っておいて欲しいのですが文字が3種類以上ある時の展開は どれか1つの文字 「等式の変形」でつまずく3つの原因 1「移項」と「係数を1にする」がごっちゃ 2「逆数をかける」で統一されてない 3文字だらけの答えでいいのか不安 指導案①：項が1コずつ 基本問題 応用問題 発展問題 難問 「等式の変形」でつまずく3つの原因 まずは「等式の変形」で中学生がつまずく原因から。 生徒たちの誤答でいちばん多いのは、この図のようなミスです↑。 なぜこんなミス3つの不等式の解き方 絶対値の不等式の解き方 （1）の絶対値解法 （2）の絶対値解法 絶対値の不等式（場合分けが必要）の解き方 応用（満たす整数を考える問題） （1）満たす自然数の値を求める （2）定数 の値の範囲を求める 二次不等式の解き方

等式の変形 解き方 分数のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

一次方程式の解の求め方 数学fun	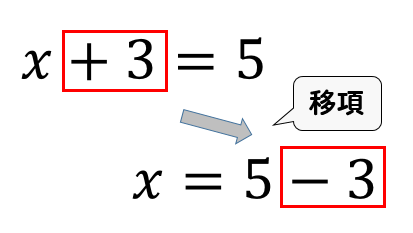一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	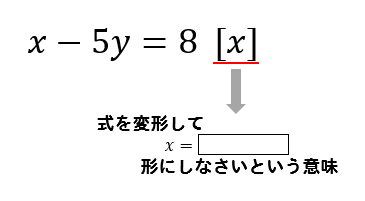一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	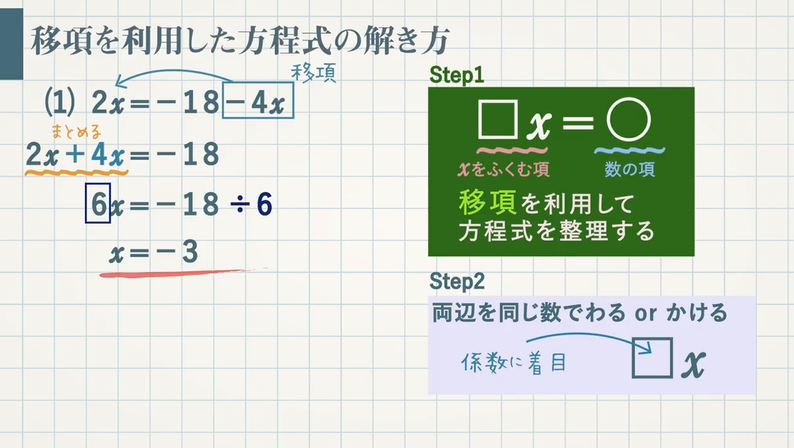一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
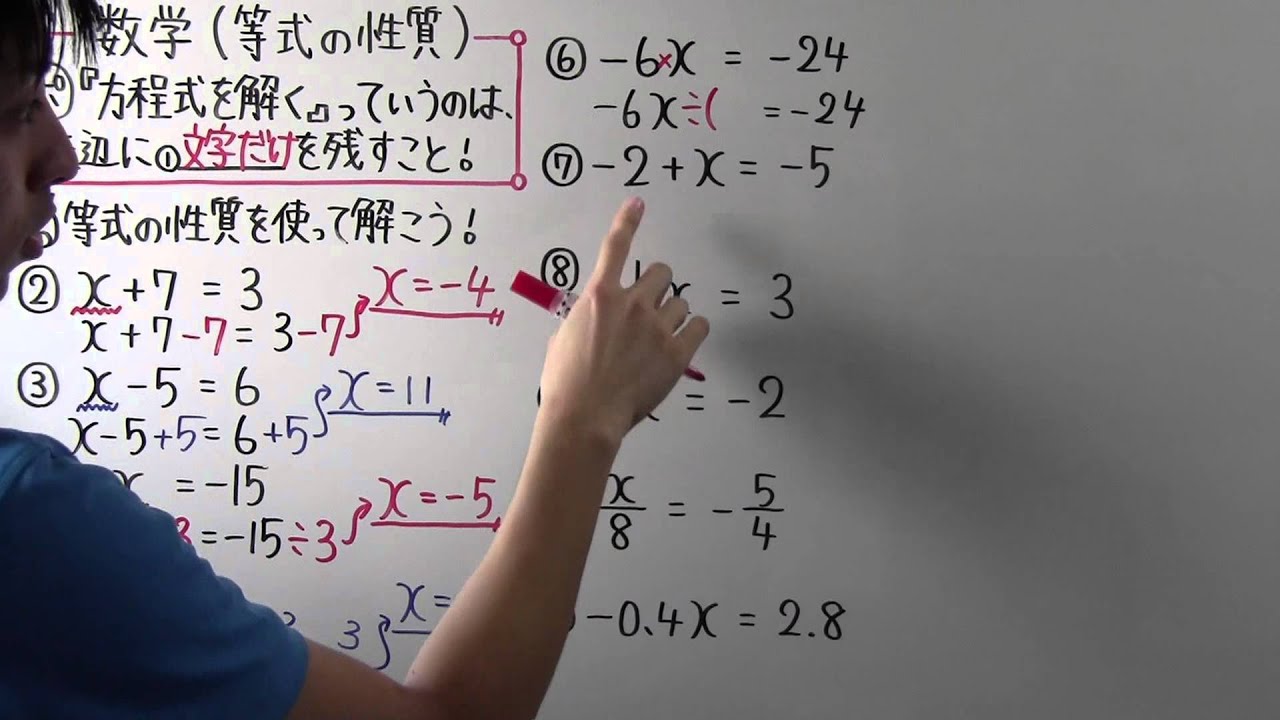一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	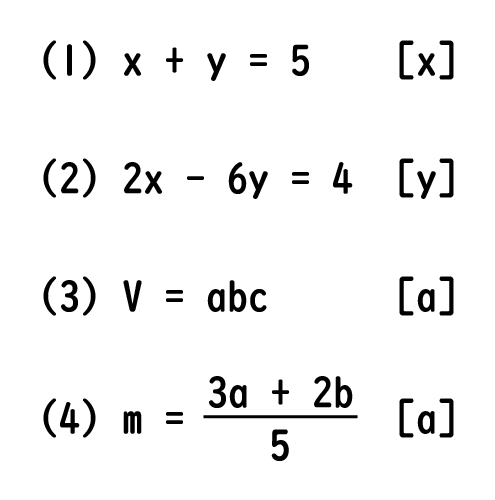一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	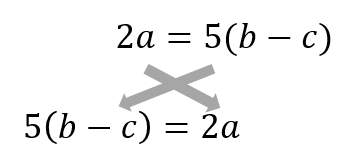一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun
一次方程式の解の求め方 数学fun	一次方程式の解の求め方 数学fun

三角関数の不等式の解き方 三角方程式の基本形（ sinθ≧c sin θ ≧ c ， cosθ≧c cos θ ≧ c ， tanθ≧ c tan θ ≧ c ， 不等号は≧，≦，＞，＜のいずれでもよい ） に式を変形して解く． aθ−b =t a θ − b = t と変数を変換することにより基本形にする．このとき こんにちは。今回は等式の変形についてです。攻め方を書いてみました。 等式変形・中1で習った方程式 等式の変形って実は中学1年生でやってるんですね。 中学1年生の等式で, 代表的なものが, 方程式です。 例えば 次の方程式を解け

Incoming Term: 等式の変形 解き方, 等式の変形 解き方 分数, 中2 数学 等式の変形 解き方,